SPRAD27A July 2022 – August 2022 AM2431 , AM2432 , AM2434 , AM2631 , AM2631-Q1 , AM2632 , AM2632-Q1 , AM2634 , AM2634-Q1 , AM2732 , AM2732-Q1 , AM6411 , AM6412 , AM6421 , AM6422 , AM6441 , AM6442
2.2.2 Optimizing Arctangent and Arctangent2
The arctangent function, and in particular, the arctangent2 function is a critical function in control applications. For example, in motor control, there may be sensors used to get the x and y position of a motor. Then, the application needs to translate that into an angular value. A standard arctan function would be called as arctan(y/x), but this loses the quadrant information as Q1 and Q3 are both positive and Q2 and Q4 are both negative. The arctan2 function accepts both the x and the y input to return a value in the full −π to π range versus the arctan function that returns values only in Q1 or Q4, −π/2 to π/2.
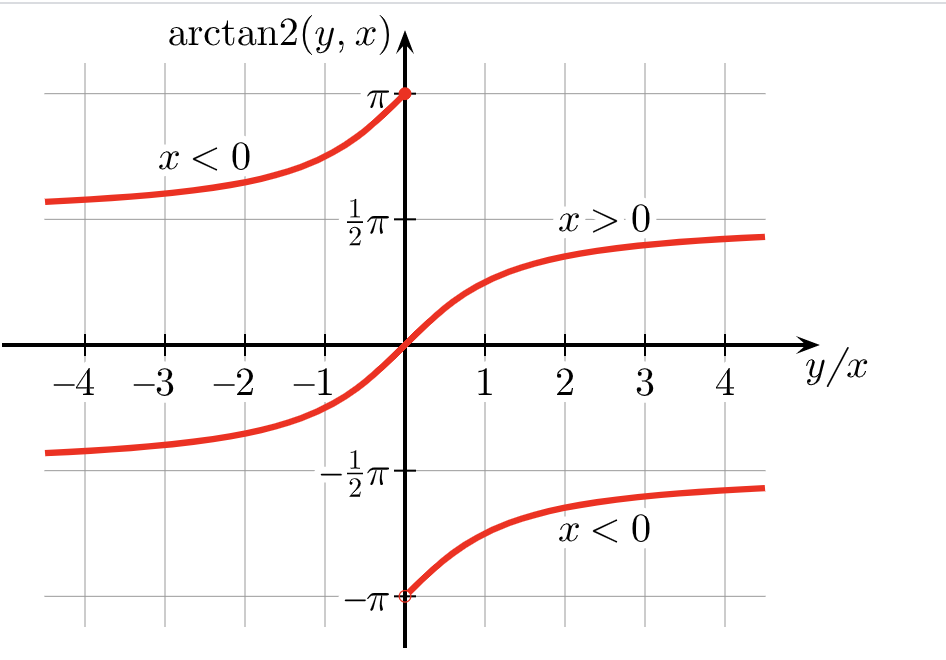 Figure 2-4 Plot of arctan2(y,x)
Figure 2-4 Plot of arctan2(y,x)As the input to arctan(z) can be any number from −∞to ∞, use trig identities to reduce the range and get an approximation function that is relatively low complexity.
Start with:
- arctan(x) = π/2- arctan(1/x) (1a)
- arctan(x)=−arctan(x) (2a)
These identities allow you to restrict the approximation range to abs(x) <=1.
The next step is to find a simple polynomial that approximates arctan in the range 0-1, or -1 to 1. Using sollya, try some different polynomial lengths to get the approximation error. This is shown in Table 2-3. You can see that the error is not falling that fast as a function of the number of terms in the polynomial, so even at 6 terms you are still at 3.4e-6 in the range (-1,1). Also note that arctan is an odd function where all the terms are odd powers.