SPRAD27A July 2022 – August 2022 AM2431 , AM2432 , AM2434 , AM2631 , AM2631-Q1 , AM2632 , AM2632-Q1 , AM2634 , AM2634-Q1 , AM2732 , AM2732-Q1 , AM6411 , AM6412 , AM6421 , AM6422 , AM6441 , AM6442
2.2.1 Optimizing Sine and Cosine
This section shows how the above techniques are applied to optimize the computations for a Sin + Cos function. Sin + Cos functions are commonly used in the transforms for control algorithms where both sin and cos are needed at the same time.
The first step in using polynomial approximations is to range reduce the input so that the segment of the function that needs to be modeled is smaller. The most common range reduction for sin/cos computation is to reduce the input to the range.
Then, compute the approximation in this region and then adjust the sign depending on which quadrant the angle was in originally. Using the Chebyshev polynomials and the fact that sin(x) is an odd function and cos(x) is an even function, you will see the following:
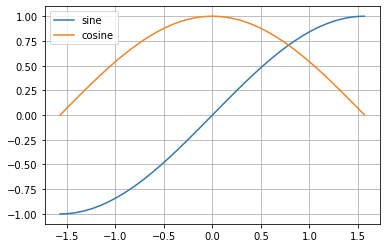 Figure 2-1 Plot of Sine and Cosine Over
the Range
Figure 2-1 Plot of Sine and Cosine Over
the RangeIf you assume that the input to the functions are limited to , you need to map the input value to the range before implementing the approximation. This can be done with a couple simple comparisons:
A further range reduction technique can be used to limit the input to using the trigonometric identities:
Which yields the following mapping for sin(x) and a similar one for cos(x):
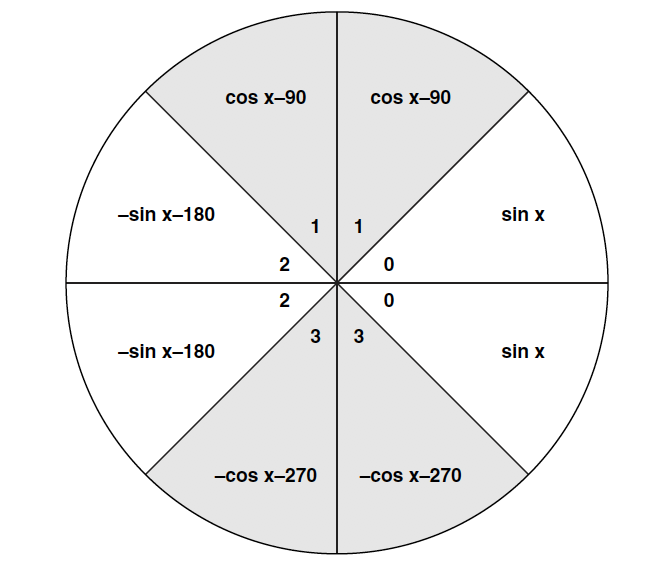 Figure 2-2 Mapping of the Unit Circle for
sin(x) for
Figure 2-2 Mapping of the Unit Circle for
sin(x) for
Since you only have to model the sine cosine from , you need fewer coefficients to achieve higher accuracy.
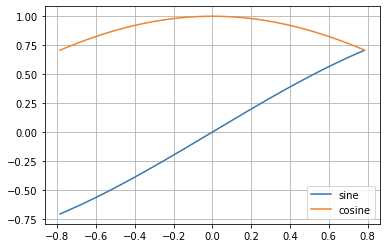 Figure 2-3 Plot of Sine and Cosine Over
the Range
Figure 2-3 Plot of Sine and Cosine Over
the Range