ZHCSFG3B July 2016 – December 2016 TPS546C20A
PRODUCTION DATA.
- 1 特性
- 2 应用范围
- 3 说明
- 4 修订历史记录
- 5 Pin Configuration and Functions
- 6 Specifications
-
7 Detailed Description
- 7.1 Overview
- 7.2 Functional Block Diagram
- 7.3
Feature Description
- 7.3.1 2-Phase Application
- 7.3.2 Linear Regulators BP3 and BP6
- 7.3.3 Input Undervoltage Lockout (UVLO)
- 7.3.4 Turnon and Turnoff Delay and Sequencing
- 7.3.5 Voltage Reference
- 7.3.6 Differential Remote Sense and Compensation
- 7.3.7 Set Output Voltage and Adaptive Voltage Scaling (AVS)
- 7.3.8 Reset VOUT
- 7.3.9 Switching Frequency and Synchronization
- 7.3.10 Current Sharing
- 7.3.11 Soft-Start Time and TON_RISE Command
- 7.3.12 Prebiased Output Start-Up
- 7.3.13 Soft-Stop time and TOFF_FALL Command
- 7.3.14 Output Current Telemetry and Low-Side MOSFET Overcurrent Protection
- 7.3.15 High-Side MOSFET Short-Circuit Protection
- 7.3.16 Die Temperature Telemetry and Overtemperature Protection
- 7.3.17 Output Voltage Telemetry and Over-/Under-voltage Protection
- 7.3.18 TON_MAX Fault
- 7.3.19 Power Good (PGOOD) Indicator
- 7.3.20 Fault Protection Responses
- 7.3.21 Switching Node
- 7.3.22 PMBus General Description
- 7.3.23 PMBus Address
- 7.3.24 PMBus Connections
- 7.3.25 Auto ARA (Alert Response Address) Response
- 7.4 Device Functional Modes
- 7.5 Programming
- 7.6
Register Maps
- 7.6.1 OPERATION (01h)
- 7.6.2 ON_OFF_CONFIG (02h)
- 7.6.3 CLEAR_FAULTS (03h)
- 7.6.4 WRITE_PROTECT (10h)
- 7.6.5 STORE_DEFAULT_ALL (11h)
- 7.6.6 RESTORE_DEFAULT_ALL (12h)
- 7.6.7 STORE_USER_ALL (11h)
- 7.6.8 RESTORE_USER_ALL (12h)
- 7.6.9 CAPABILITY (19h)
- 7.6.10 SMBALERT_MASK (1Bh)
- 7.6.11 VOUT_MODE (20h)
- 7.6.12 VOUT_COMMAND (21h)
- 7.6.13 VOUT_MAX (24h)
- 7.6.14 VOUT_TRANSITION_RATE (27h)
- 7.6.15 VOUT_SCALE_LOOP (29h)
- 7.6.16 VOUT_MIN (2Bh)
- 7.6.17 VIN_ON (35h)
- 7.6.18 VIN_OFF (36h)
- 7.6.19 IOUT_CAL_OFFSET (39h)
- 7.6.20 VOUT_OV_FAULT_RESPONSE (41h)
- 7.6.21 VOUT_UV_FAULT_RESPONSE (45h)
- 7.6.22 IOUT_OC_FAULT_LIMIT (46h)
- 7.6.23 IOUT_OC_FAULT_RESPONSE (47h)
- 7.6.24 IOUT_OC_WARN_LIMIT (4Ah)
- 7.6.25 OT_FAULT_LIMIT (4Fh)
- 7.6.26 OT_FAULT_RESPONSE (50h)
- 7.6.27 OT_WARN_LIMIT (51h)
- 7.6.28 TON_DELAY (60h)
- 7.6.29 TON_RISE (61h)
- 7.6.30 TON_MAX_FAULT_LIMIT (62h)
- 7.6.31 TON_MAX_FAULT_RESPONSE (63h)
- 7.6.32 TOFF_DELAY (64h)
- 7.6.33 TOFF_FALL (65h)
- 7.6.34 STATUS_BYTE (78h)
- 7.6.35 STATUS_WORD (79h)
- 7.6.36 STATUS_VOUT (7Ah)
- 7.6.37 STATUS_IOUT (7Bh)
- 7.6.38 STATUS_INPUT (7Ch)
- 7.6.39 STATUS_TEMPERATURE (7Dh)
- 7.6.40 STATUS_CML (7Eh)
- 7.6.41 STATUS_MFR_SPECIFIC (80h)
- 7.6.42 READ_VOUT (8Bh)
- 7.6.43 READ_IOUT (8Ch)
- 7.6.44 READ_TEMPERATURE_1 (8Dh)
- 7.6.45 PMBUS_REVISION (98h)
- 7.6.46 IC_DEVICE_ID (ADh)
- 7.6.47 IC_DEVICE_REV (AEh)
- 7.6.48 MFR_SPECIFIC_00 (D0h)
- 7.6.49 VREF_TRIM (MFR_SPECIFIC_04) (D4h)
- 7.6.50 STEP_VREF_MARGIN_HIGH (MFR_SPECIFIC_05) (D5h)
- 7.6.51 STEP_VREF_MARGIN_LOW (MFR_SPECIFIC_06) (D6h)
- 7.6.52 PCT_OV_UV_WRN_FLT_LIMITS (MFR_SPECIFIC_07) (D7h)
- 7.6.53
OPTIONS (MFR_SPECIFIC_21) (E5h)
- 7.6.53.1 DIS_NEGILIM Bit
- 7.6.53.2 EN_RESET_B Bit
- 7.6.53.3 EN_ADC_CNTL Bit
- 7.6.53.4 VSM Bit
- 7.6.53.5 DLO Bit
- 7.6.53.6 AVG_PROG[1:0] Bits
- 7.6.53.7 EN_AUTO_ARA Bit
- 7.6.53.8 READ_VOUT_RANGE[1:0] Bits
- 7.6.53.9 EN_DRV_IV_VSEL Bit
- 7.6.53.10 RST_VOUT_oSD Bit
- 7.6.53.11 DIS_VSEL Bit
- 7.6.53.12 RSMLO_VAL Bit
- 7.6.53.13 RSMHI_VAL Bit
- 7.6.54 MISC_CONFIG_OPTIONS (MFR_SPECIFIC_32) (F0h)
-
8 Applications and Implementation
- 8.1 Application Information
- 8.2
Typical Application
- 8.2.1
4.5-V to 18-V Input, 1-V Typical Output, 35-A Converter
- 8.2.1.1 Design Requirements
- 8.2.1.2
Detailed Design Procedure
- 8.2.1.2.1 Switching Frequency Selection
- 8.2.1.2.2 Inductor Selection
- 8.2.1.2.3 Output Capacitor Selection
- 8.2.1.2.4 Output Voltage Deviation During Load Transient
- 8.2.1.2.5 Output Voltage Ripple
- 8.2.1.2.6 Input Capacitor Selection
- 8.2.1.2.7 AVIN, BP6, BP3 Bypass Capacitor
- 8.2.1.2.8 Bootstrap Capacitor Selection
- 8.2.1.2.9 R-C Snubber
- 8.2.1.2.10 Output Voltage Setting and Frequency Compensation Selection
- 8.2.1.2.11 Key PMBus Parameter Selection
- 8.2.1.2.12 Enable, UVLO
- 8.2.1.2.13 Soft-Start Time
- 8.2.1.2.14 Overcurrent Threshold and Response
- 8.2.1.3 Application Curves
- 8.2.1
4.5-V to 18-V Input, 1-V Typical Output, 35-A Converter
- 9 Power Supply Recommendations
- 10Layout
- 11器件和文档支持
- 12机械、封装和可订购信息
8 Applications and Implementation
NOTE
Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.
8.1 Application Information
The TPS546C20A devices are highly-integrated, synchronous step-down DC-DC converters. These devices are used to convert a higher DC-input voltage to a lower DC-output voltage, with a maximum output current of 35 A. Use the following design procedure to select key component values for this device, and set the appropriate behavioral options through the PMBus.
8.2 Typical Application
8.2.1 4.5-V to 18-V Input, 1-V Typical Output, 35-A Converter
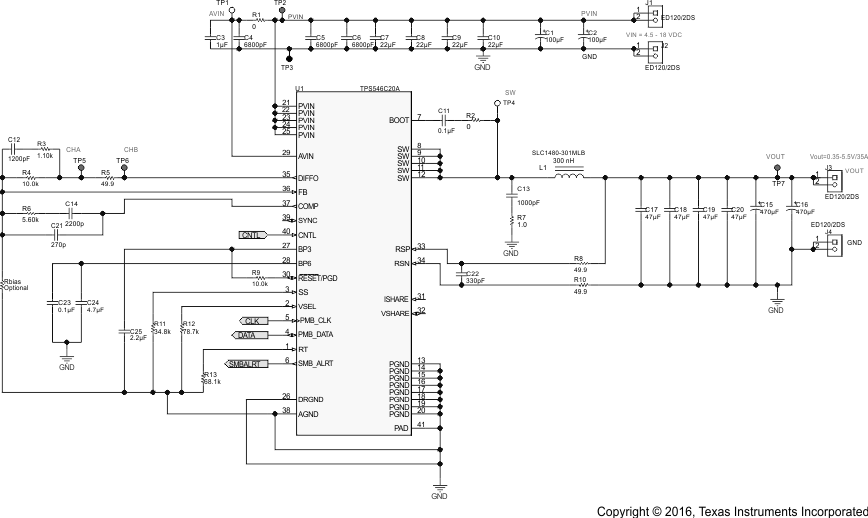 Figure 39. Typical Application Schematic, TPS546C20A
Figure 39. Typical Application Schematic, TPS546C20A
8.2.1.1 Design Requirements
For this design example, use the input parameters listed in Table 15.
Table 15. Design Parameters
| DESIGN PARAMETER | TEST CONDITIONS | MIN | TYP | MAX | UNIT | |
|---|---|---|---|---|---|---|
| VIN | Input voltage | 4.5 | 12 | 18 | V | |
| VIN(ripple) | Input ripple voltage | IOUT = 35 A | 0.3 | V | ||
| VOUT | Output voltage | 1 | V | |||
| ΔVO(ΔVI) | Line regulation | 4.5 V ≤ VIN ≤ 18 V | 0.5% | |||
| ΔVO(ΔIO) | Load regulation | 0 V ≤ IOUT ≤ 35 A | 0.5% | |||
| VPP | Output ripple voltage | IOUT = 35 A | 12 | mV | ||
| ∆VOUT | VOUT deviation during load transient | ∆IOUT = 10 A, Vin = 12 V | 30 | mV | ||
| IOUT | Output current | 4.5 V ≤ VIN ≤ 18 V | 0 | 35 | A | |
| tSS | Soft-start time | 5 | ms | |||
| IOC | Output overcurrent trip point | 40 | A | |||
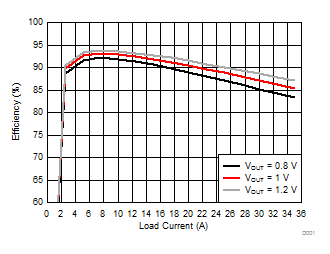
| η | Efficiency | VOUT = 1 V, IOUT = 17 A, VIN = 12 V | 90% | |||
| fSW | Switching frequency | 300 | kHz | |||
8.2.1.2 Detailed Design Procedure
8.2.1.2.1 Switching Frequency Selection
There is a tradeoff between higher and lower switching frequencies for buck converters. Higher switching frequencies may produce smaller solution size using lower valued inductors and smaller output capacitors compared to a power supply that switches at a lower frequency. However, the higher switching frequency causes extra switching losses, which decrease efficiency and impact thermal performance. In this design, a moderate switching frequency of 300 kHz achieves both a small solution size and a high-efficiency operation. With the frequency selected, use Equation 15 to calculate the timing resistor (RT). The standard value of 68.1 kΩ is used in the design.
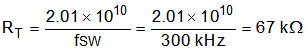
8.2.1.2.2 Inductor Selection
Use Equation 16 to calculate the value of the output inductor (L). The coefficient, KIND, represents the amount of inductor-ripple current relative to the maximum output current. The output capacitor filters the inductor-ripple current. Therefore, selecting a high inductor-ripple current impacts the selection of the output capacitor because the output capacitor must have a ripple-current rating equal to or greater than the inductor-ripple current. Generally, the KIND coefficient should be kept between 0.2 and 0.3 for balanced performance. Using this target ripple current, the required inductor size can be calculated as shown in Equation 16.
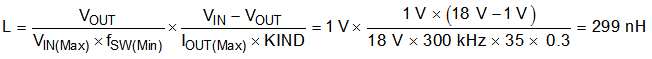
Selecting a value of 0.3 for the KIND coefficient, the target inductance, L, is 299 nH. Considering the variation and derating of the inductance and the 300-nH inductor, use Equation 17, Equation 18, and Equation 19 to calculate the inductor-ripple current (IRIPPLE), RMS current (IL(rms)), and peak current (IL(peak)), respectively. These values should be used to select an inductor with approximately the target inductance value, and current ratings that allow normal operation with some margin.
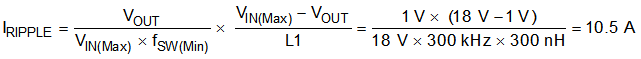
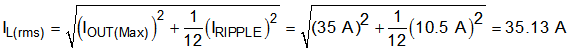
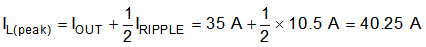
Considering the required inductance, RMS current, and peak current, the 300-nH inductor, SLC1480-301ML, from Coilcraft was selected for this application.
8.2.1.2.3 Output Capacitor Selection
Consider the following when selecting the value of the output capacitor:
- The output-voltage deviation during load transient
- The output-voltage ripple
8.2.1.2.4 Output Voltage Deviation During Load Transient
The desired response to a load transient is the first criterion for output capacitor selection. The output capacitor must supply the load with the required current when not immediately provided by the regulator. When the output capacitor supplies load current, the impedance of the capacitor affects the magnitude of the voltage deviation during the transient.
To meet the requirements for control-loop stability, the device requires the addition of compensation components in the design of the error amplifier. While these compensation components provide for a stable control loop, they often also reduce the speed with which the regulator can respond to load transients. The delay in the regulator response to load changes can be two or more clock cycles before the control loop reacts to the change. During that time, the difference (delta) between the old and the new load current must be supplied (or absorbed) by the output capacitance. The output capacitor impedance must be designed to supply or absorb the delta current while maintaining the output voltage within acceptable limits. Equation 20 and Equation 21 show the relationship between the transient response overshoot (VOVER), the transient response undershoot (VUNDER), and the required output capacitance (COUT).
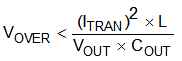
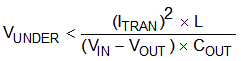
If
- VIN(min) > 2 × VOUT, use overshoot to calculate minimum output capacitance.
- VIN(min) < 2 × VOUT, use undershoot to calculate minimum output capacitance.
In this case, the minimum designed input voltage, VIN(min), is greater than 2 × VOUT, so VOVER dictates the minimum output capacitance. Therefore, using Equation 22, the minimum output capacitance required to meet the transient requirement is 1000 µF.
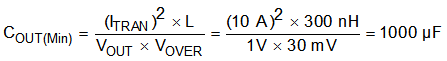
8.2.1.2.5 Output Voltage Ripple
The output-voltage ripple is the second criterion for output capacitor selection. Use Equation 23 to calculate the minimum output capacitance required to meet the output-voltage ripple specification.
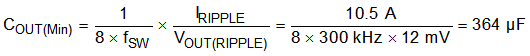
In this case, the target maximum output-voltage ripple is 12 mV. Under this requirement, the minimum output capacitance for ripple is 330 µF. Because this capacitance value is smaller than the output capacitance required for the transient response, select the output capacitance value based on the transient requirement. Considering the variation and derating of capacitance, in this design, two 470-µF low-ESR polymer bulk capacitors and four 47-µF ceramic capacitors were selected to meet the transient specification with sufficient margin. Therefore COUT is equal to 1128 µF.
With the target output capacitance value selected, use Equation 24 to calculate the maximum ESR that the output-capacitor bank allows to meet the output-voltage ripple specification. Equation 24 indicates the ESR should be less than 1.3 mΩ. Each 470-µF ceramic capacitor contributes approximately 1.3 mΩ, making the effective ESR of the output capacitor bank approximately 0.65 mΩ which is within the specification with sufficient margin.
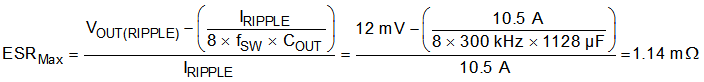
8.2.1.2.6 Input Capacitor Selection
The power-stage input-decoupling capacitance (effective capacitance at the PVIN and PGND pins) must be sufficient to supply the high switching currents demanded when the high-side MOSFET switches on, while providing minimal input-voltage ripple as a result. This effective capacitance includes any DC-bias effects. The voltage rating of the input capacitor must be greater than the maximum input voltage with derating. The capacitor must also have a ripple-current rating greater than the maximum input-current ripple to the device during full load. Use Equation 25 to estimate the input RMS current.
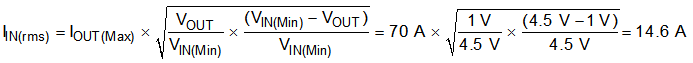
The minimum input capacitance and ESR values for a given input voltage-ripple specification, VIN(ripple), are shown in Equation 26 and Equation 27. The input ripple is composed of a capacitive portion (VRIPPLE(cap)) and a resistive portion (VRIPPLE(esr)).
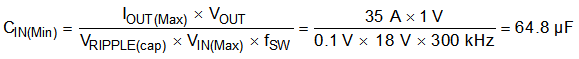
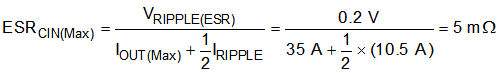
The value of a ceramic capacitor varies significantly over temperature and the amount of DC bias applied to the capacitor. The capacitance variations because of temperature can be minimized by selecting a dielectric material that is stable over temperature. X5R and X7R ceramic dielectrics are usually selected for power-regulator capacitors because these components have a high capacitance-to-volume ratio and are fairly stable over temperature. The input capacitor must also be selected with consideration of the DC bias. For this example design, a ceramic capacitor with at least a 25-V voltage rating is required to support the maximum input voltage. For this design, allow 0.1-V input ripple for VRIPPLE(cap) and 0.2-V input ripple for VRIPPLE(esr). Using Equation 26 and Equation 27, the minimum input capacitance for this design is 64.8 µF, and the maximum ESR is 5 mΩ. For this design example, four 22-μF, 25-V ceramic capacitors, three 6800-pF, 25-V ceramic capacitors, and two additional 100-μF, 25-V low-ESR electrolytic capacitors in parallel were selected for the power stage with sufficient margin.
A high-frequency PVIN-bypass capacitor is suggested to be placed close to power stage to help with ringing reduction. .
8.2.1.2.7 AVIN, BP6, BP3 Bypass Capacitor
The BP3 pin requires a minimum capacitance of 2.2 µF connected to AGND. The BP6 pin should have approximately 4.7 µF of capacitance connected to PGND. The PVIN pin should have approximately 1 µF of capacitance connected to PGND. To filter ripple on the AVIN pin, a small value resistor is recommended to be placed between PVIN pin and AVIN.
8.2.1.2.8 Bootstrap Capacitor Selection
A ceramic capacitor with a value of 0.1 μF must be connected between the BOOT and SW pins for proper operation. TI recommends using a ceramic capacitor with X5R or better grade dielectric. The capacitor should have voltage rating of 25 V or higher.
8.2.1.2.9 R-C Snubber
An R-C snubber must be placed between the switching node and PGND to reduce voltage spikes on the switching node. The power rating of the resistor must be larger than the power dissipation on the resistor with sufficient margin. To balance efficiency and spike level, a 1-nF capacitor and a 1-Ω resistors were selected for this design.
In this example an 0805 resistor was selected, which is rated for 0.125 W.
8.2.1.2.10 Output Voltage Setting and Frequency Compensation Selection
The device uses voltage-mode control with input feedforward. For an in-depth discussion of voltage-mode feedback and control, refer to Under the Hood of Low-Voltage DC/DC Converters (SLUP206). Frequency compensation can be accomplished using standard techniques. TI also provides a compensation calculator tool as part of the WEBENCH® selection simulation services to streamline compensation design. The tool provides the recommended compensation components and approximate bode plots. As a starting point, set the crossover frequency to 1/10 fSW and 2 to 5 times the resonant frequency of the output LC filter. The phase margin at crossover should be greater than 45°. The resulting plots should be reviewed for a few common considerations. The error-amplifier gain should not hit the error amplifier gain bandwidth product (GBWP). The error-amplifier gain at the switching frequency region is recommended to be approximately 6 dB in general. The high-frequency capacitor from the COMP to FB pins for this device must be above a typical value of 100 pF to 150 pF to lower the high-frequency gain for stability. Use the tool to calculate the system bode plot at different loading conditions to ensure that the phase does not drop below zero prior to crossover, as this condition is known as conditional stability.
The design tool provides the compensation network values as a start point. Measuring the real-system bode plot after the design and adjusting the compensation values accordingly is always recommended. Table 16 lists the compensation values from the tool calculation and optimization based on the measured data.
Table 16. Frequency Compensation Values
| RESISTOR | VALUE (kΩ) | CAPACITOR | VALUE (pF) |
|---|---|---|---|
| R4 | 10 | C12 | 1200 |
| R3 | 1.1 | C14 | 2200 |
| R6 | 5.6 | C21 | 270 |
| RBias | Open | — | — |
8.2.1.2.11 Key PMBus Parameter Selection
Some key design parameters for the device can be configured through PMBus, and stored to the non-volatile memory (NVM) for future use.
8.2.1.2.12 Enable, UVLO
The ON_OFF_CONFIG command is used to select the turnon behavior of the converter. For this example, the CNTL pin was used to enable or disable the converter, regardless of the state of OPERATION, as long as the input voltage is present and above the UVLO threshold. The CNTL pin is pulled to the BP6 pin through an internal 6-µA current source if it is floating.
8.2.1.2.13 Soft-Start Time
The TON_RISE command sets the soft-start time. The charging current for the output capacitors must be considered when selecting the soft-start time. In some applications (for example, those with large amounts of output capacitance) this current can lead to false tripping of the overcurrent-protection circuitry if the soft-start time is not properly selected. To avoid false tripping, the output capacitor-charging current should be included when selecting a soft-start time and overcurrent threshold. Use Equation 28 to calculate the capacitor-charging current (ICAP).
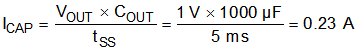
In this example, the soft-start time is selected to be the default value of 5 ms. In this case, the charging current, ICAP, is 0.23 A.
8.2.1.2.14 Overcurrent Threshold and Response
The IOUT_OC_FAULT_LIMIT command sets the overcurrent threshold. The device uses inductor middle current value for overcurrent detecting. The current limit should be set to the maximum load current, plus the output capacitor charging current during start-up, plus some margin for load transients and component variation. The amount of margin required depends on the individual application, but a suggested point is between 20% and 40%. For this application, the maximum load current is 35 A, the output capacitor charging current is 0.44 A. This design allows some extra margin, so an overcurrent threshold of 40 A was selected.
The IOUT_OC_FAULT_RESPONE command sets the desired response to an overcurrent event. In this example, the converter is configured to hiccup in the event of an overcurrent. The device can also be configured to latch in the event of an overcurrent.
8.2.1.3 Application Curves
| VIN = 5 V | L = 300 nH | Snubber = 1 nF + 1 Ω |
| fSW = 300 kHz | RDCR = 0.2 mΩ | RBOOT = 0 Ω |
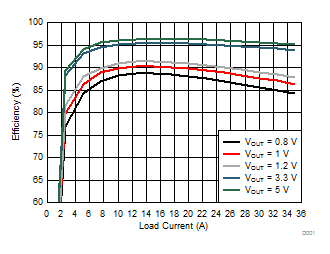
| VIN = 12 V | L = 300 nH | Snubber = 1 nF + 1 Ω |
| fSW = 300 kHz | RDCR = 0.2 mΩ | RBOOT = 0 Ω |
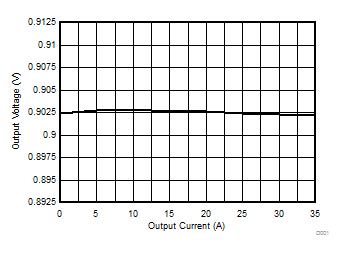
| VIN = 12 V | VOUT = 0.9 V |
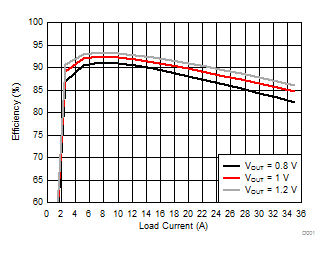
| VIN = 5 V | L = 300 nH | Snubber = 1 nF + 1Ω |
| fSW = 500 kHz | RDCR = 0.2 mΩ | RBOOT = 0 Ω |
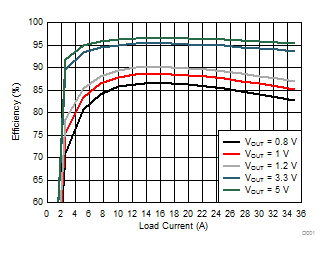
| VIN = 12 V | L = 300 nH | Snubber = 1 nF + 1Ω |
| fSW = 500 kHz | RDCR = 0.2 mΩ | RBOOT = 0 Ω |
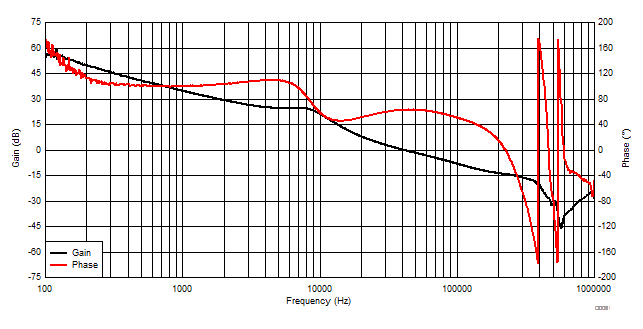
| VIN = 12 V | VOUT = 0.9 V | IOUT = 20 A |
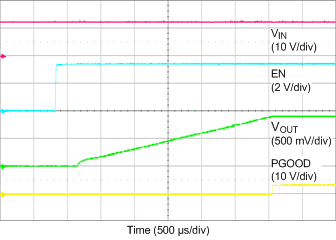
| VIN = 12 V | VOUT = 0.9 V | IOUT = 20 A |
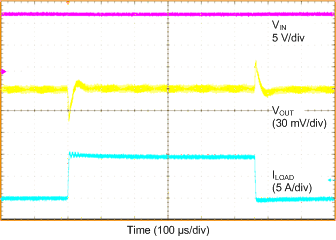
| VIN = 12 V | VOUT = 0.9 V | IOUT = 0 A to 10 A, 2.5 A/µs |
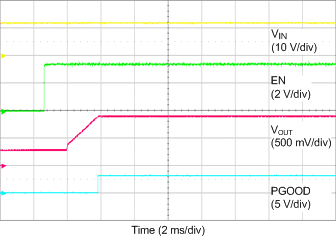
| VIN = 12 V | IOUT = 0 A | |
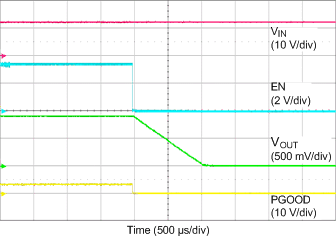
| VIN = 12 V | VOUT = 0.9 V | IOUT = 20 A |
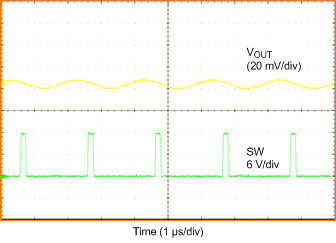
| VIN = 12 V | VOUT = 0.9 V | IOUT = 20 A |
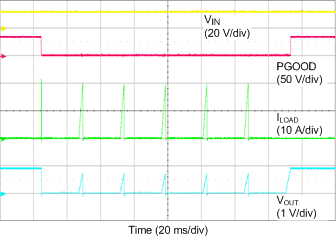
| VIN = 12 V | IOUT = 0 A to 20 A, 20 A to 0 A | |
| Set OCF = 18 A | VOUT = 0.9 V | |